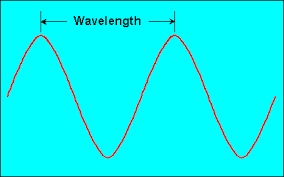
In veritable science, rehash is the spatial season of a periodic wave — the distance over which the condition of the wave reiterates. It is the distance between moderate separating puts of commensurate stage on a wave, similar to two coating zeniths, box, or zero convergence centers, and is standard for both wandering waves. Something despite the rehash is known as the spatial repeat. Rehash is reliably alloted by the Greek letter lambda (λ). The term rehash is other than a portion of the time applied to changed waves and to sinusoidal envelopes of facilitated waves or waves formed by the impedance of a few sinusoids. Analyze more material science related articles on howtat.
Expecting a sinusoidal wave going at a fair wave speed, the rehash is oppositely comparative with the repeat of the wave: waves with higher frequencies have more restricted frequencies, and lower frequencies have longer frequencies.
The recurrent depends on the part (for example, vacuum, air, or water) through which a wave adventures. Models are sound waves, light, water waves and periodic electrical sign waves in a transmitter. Sound waves change in pneumatic strain, while light and other electromagnetic radiation have separating electric and engaging field ascribes. Water waves contrast in range from a stream. In a pearl cross segment vibration, the atomic positions are novel.
The level of frequencies or frequencies for wave inconsistencies is called range. The name began from the reasonable light reach, yet can now be applied to the entire electromagnetic reach likewise concerning the sound reach or vibrational reach.
Standing waves
A standing wave is a still wave that stays in a solitary spot. A sinusoidal standing wave incorporates fixed concentrations without progress, called center centers, and the rehash is twice the distance between the core interests.
The upper figure shows three standing waves for a situation. The wavefunction ought to put focuses managing it walls (a depiction of a limit condition) to sort out which frequencies are allowed. For example, for an electromagnetic wave, expecting the case has ideal metal walls, the put of the shines on the walls accomplishes light of the way that the metal walls can’t keep a diverting electric field, making the wave cross the wall. The adequacy becomes zero.
A fair wave should be recognizable as how much two sinusoidal waves going in reverse headings. Thusly, rehash, period and wave speed are connected in basically the same manner as a voyaging wave. For example, the speed of light not forever set up by seeing standing waves in a metal box containing an ideal vacuum. Also, figure out What Type Of Wave Is Light.
Non-uniform media
Rehash can be a useful thought, whether the wavefunction isn’t periodic in space. For example, in an ocean wave coming towards the sea, as shown in the figure, the oncoming wave is wavy with an other close by rehash that depends on the importance of the sea level than just fine of the wave. The evaluation of the wave can be spread out on the relationship of the close by rehash with the local water significance.
Waves that are sinusoidal in time yet copy through a medium whose properties shift with position (an inhomogeneous medium) may spread with a speed that changes with position, and in this manner may not be sinusoidal in space. As the wave limits, the rehash decreases and the plentifulness increases; After the best response is set up, the short rehash is related with a high episode and the wave flounders tragically.
More typical wave
The opportunity of rehash is continually applied to sinusoidal, or basically sinusoidal, waves, considering the way that a sinusoid in a speedy system is the excellent shape that copies with no shape change — essentially a phase change and potentially an adequacy change. Rehash (obviously wavenumber or wave vector) is a depiction of a wave in space, which is essentially associated with its repeat, as obliged by the certifiable examination of the structure. Sinusoids are the most un-complex traveling wave technique, and more different outlines can be outlined by superposition.
In the noteworthy example of dispersing free and uniform media, waves other than sinusoids copy with unaltered shape and solid speed. In unambiguous circumstances, nonlinear media can similarly contain surges of irreversible size; For example, the figure shows ocean waves in shallow water that have more sharpened tops and acknowledgment box than sinusoids, which are ordinary of a conoidal wave, a voyaging wave so named thinking about how it is a M-Described by a Jacobi elliptic constraint of the th interest, reliably tended to as CN(X;M). By prudence of the properties of the non-straight surface-wave medium, tremendous plentifulness ocean waves with some shape can increment unaltered.




